Las chaperonas son proteínas que ayudan al plegamiento de otras proteínas recién formadas. ¿Alteran las chaperonas el espacio de búsqueda del plegamiento o sólo aceleran la búsqueda del óptimo? Un nuevo artículo en Nature apunta a la primera opción. Las chaperonas alteran el espacio de búsqueda impidiendo la exploración de regiones asociadas a plegamientos incorrectos. El nuevo resultado se ha obtenido gracias al estudio de una chaperona llamada factor desencadente (TF) en la bacteria Escherichia coli mediante el microscopio de fuerza atómica y las pinzas ópticas; estas herramientas permiten estudiar el plegamiento de proteínas en una sola molécula, incluyendo la observación de los estados transitorios durante el plegado y las transiciones entre ellos. Futuros estudios tendrán que aclarar si lo mismo ocurre con otras chaperonas. El artículo técnico es Alireza Mashaghi et al., “Reshaping of the conformational search of a protein by the chaperone trigger factor,” Nature 500: 98–101, 01 Aug 2013.

En ausencia de la chaperona (-TF) la relación entre la fuerza y la extensión es simple con dos transiciones, una pequeña a los 10 pN (picoNewton) y otra más grande a los 22 pN. En presencia de la chaperona (+TF), unos 1 μM, las curvas son mucho más complicadas, mostrando nuevos estados intermedios; estos nuevos picos en el diagrama fuerza-extensión sugieren que las proteínas adoptan nuevos estados parcialmente plegados. En estos nuevos picos se llegan a alcanzar fuerzas de hasta 40  pN, mucho mayores que la fuerza pico sin chaperona de 22  ±  5  pN.

Los autores interpretan sus resultados como que el paisaje energético que se explora durante el plegamiento cambia bajo la presencia de la chaperona TF, apareciendo nuevos “mínimos locales” y cambiando la profundidad de los existentes. El estudio sugiere que la chaperona se acopla a una parte concreta del polipéptido protegiendo esta región de su interacción con las partes mal plegadas distantes. Por supuesto, futuros estudios tendrán que confirmar esta interpretación y comprobar si también explica el comportamiento de otras chaperonas.

En la electrodinámica cuántica (QED) el grupo U(1)_em puede ser trivial, igual a SU(1), o no trivial, en cuyo caso las ecuaciones de Maxwell deben incluir un monopolo magnético de Dirac. En la teoría electrodébil (EW) el grupo SU(2)×U(1)_Y se rompe en U(1)_em gracias al mecanismo de Higgs; el origen de este U(1)_em es una combinación del grupo U(1)_Y, que puede ser trivial, y del subgrupo U(1) del grupo SU(2), que no es trivial y contiene un monopolo de ‘t Hooft-Polyakov. Por tanto, el grupo U(1)_em tras la rotura de simetría electrodébil debe ser no trivial y el modelo estándar debe presentar un monopolo magnético electrodébil, llamado monopolo de Cho-Maison, que es una combinación de los monopolos de Dirac y de ‘t Hooft-Polyakov. En muchos libros se afirma, quizás a la ligera, que la teoría EW no predice ningún monopolo electrodébil porque en la rotura de simetría se puede hacer que U(1)_em sea igual a U(1)_Y, sin contenido alguno del subgrupo U(1) de SU(2); pero esta elección no es “natural” y no está justificada por ninguna razón física o matemática (salvo eliminar de forma explícita la existencia del monopolo). El monopolo electrodébil de Cho-Maison tiene una carga magnética (4π)/e, en lugar de (2π)/e como el monopolo de Dirac, porque su origen es el subgrupo U(1) de SU(2) que tiene periodo 4π en lugar de 2π. Usando una masa de 125 GeV para el bosón de Higgs, se estima que la masa del monopolo de Cho-Maison es de 3,85 TeV, sin tener en cuenta las correcciones cuánticas, que podrían subir esta masa hasta 6,72 TeV. La búsqueda de este monopolo con masa entre 4 y 7 TeV es la tarea emprendida por el experimento MoEDAL en el LHC que empezará a tomar datos en 2015 y se instalará junto a LHCb. Nos lo cuentan Y. M. Cho, J. L. Pinfold, “Electroweak Monopole Production at the LHC – a Snowmass White Paper,” arXiv:1307.8390, Subm. 31 Jul 2013.

El experimento MoEDAL será el séptimo experimento del LHC y se instalará junto al detector de vértices (VELO) del experimento LHCb, en el punto 8 de cruce de haces. Su objetivo es buscar nueva física que se manifieste como partículas altamente ionizadas, como el monopolo de Cho-Maison (cuya ionización es unas 5000 veces mayor que la producida por un protón moviéndose a la misma velocidad). Se espera que inicie la toma de datos en 2015 cuando el LHC opere en modo colisiones protón-protón a 13 TeV c.m. (o en el mejor caso a 14 TeV).

Los monopolos electrodébiles tienen una gran carga magnética y son absorbidos muy rápido por la parte más interior de los detectores ATLAS y CMS, lo que impide su detección cuando tienen una carga eléctrica o magnética muy alta. El experimento MoEDAL explorará una región más grande de posibles parámetros, de hecho, gran parte del rango de posibles masas del monopolo de Cho-Maison será explorado por MoEDAL.

El monopolo, como el bosón de Higgs, es una predicción del modelo estándar. Aún así, creo que no es exagerado afirmar que su descubrimiento sería más revolucionario.

El recocido cuántico (“quantum annealing”) es una forma de computación cuántica para la resolución de problemas de optimización combinatoria que presenta grandes ventajas (speedups) en algunos algoritmos respecto a las implementaciones basadas en el recocido simulado clásico (“simulated annealing”). Pero esta técnica no es ventajosa con un gran número de cubits sino se usan técnicas de corrección de errores. La nueva técnica llamada QAC se ha mostrado usando 344 cubits superconductores en los ordenadores D-Wave One (“Rainier”) y D-Wave Two (“Vesuvius”) de la compañía canadiense D-Wave Systems. El problema resuelto se codifica con 86 cubits, siendo el resto de los cubits necesarios para la corrección de errores. El artículo técnico, para los interesados en los detalles, es Kristen L. Pudenz, Tameem Albash, Daniel A. Lidar, “Error corrected quantum annealing with hundreds of qubits,” arXiv:1307.8190, Subm. 31 Jul 2013.

El algoritmo de recocido cuántico consiste en “cablear” el grafo del problema combinatorio a resolver en el hamiltoniano de un sistema cuántico (como muestra la figura que abre esta entrada). Los mínimos del hamiltoniano corresponderán a posibles soluciones y el algoritmo de recocido cuántico permite escapar de mínimos locales recorriendo de forma cuántica todo el espacio de configuraciones con objeto de encontrar el mínimo global (la solución óptima del problema). El recocido cuántico tiene la ventaja respecto a otros algoritmos cuánticos que no depende del entrelazamiento cuántico, aprovechando en su lugar el efecto túnel y las superposiciones cuánticas transitorias que ocurran durante la ejecución del algoritmo. Aún así, los errores debidos a la decoherencia y al entorno degradan la probabilidad de que el algoritmo acabe encontrando un óptimo y se necesitan técnicas de corrección de errores.

Para un problema “fácil” la nueva técnica de correcciones de errores logra un valor correcto el 100% de las veces para problemas con menos de 40 cubits y una tasa cercana al 90% para 86 cubits (curva “Complete (QAC)” en la figura). Hay que destacar que para este problema, cuando no se usa la técnica de corrección de errores (curva “Unprotected (U)” en la figura) la tasa de acierto del recocido cuántico es menor que para el recocido simulado clásico (curva “Classical (C)” en la figura).

Pero para un problema un “poco más difícil” la nueva técnica de correcciones de errores sólo logra un valor correcto el 20% de las veces para problemas con 86 cubits. Por supuesto, no usar corrección de errores (curva “Unprotected (U)” en la figura) o usar recocido simulado clásico (curva “Classical (C)” en la figura) conduce a una probabilidad de éxito mucho más pequeña. Me gustaría destacar un pequeño detalle de esta figura. La predicción teórica (curva continua) para el algoritmo de recocido cuántico sin corrección de errores indica que este algoritmo es mejor que el algoritmo clásico para más de 70 cubits, sin embargo, en la práctica resulta que son más o menos iguales; cualquier persona “mal pensada” diría que el algoritmo cuántico sin corrección de errores en realidad es una implementación “cuántica” del algoritmo clásico para más de 75 cubits. No seamos mal pensados.

La gran cuestión abierta, si los ordenadores de D-Wave Systems serán algún día ordenadores cuánticos de propósito general basados en computación adiabática, sigue tan abierta como el del anuncio oficial del primer ordenador “cuántico” comercial en febrero de 2007.

La noticia “Primeros indicios experimentales de una nueva física más allá del modelo estándar,” Agencia SINC, 31 Jul 2013, ha colmado muchos medios. “Físicos de la Universitat Autònoma de Barcelona (UAB) y del CNRS francés han predicho desviaciones en la probabilidad de una de las desintegraciones del mesón B que han sido detectadas en el acelerador LHC del CERN. Su confirmación será la primera prueba directa de la existencia de la “nueva física” [más allá del] modelo estándar de las partículas.” La predicción de Joaquim Matias y Javier Virto de la UAB, y Sébastien Descotes-Genon (CNRS / Université Paris-Sud) “ha sido confirmada el 19 de julio pasado en la conferencia internacional de física de partículas EPS 2013 de Estocolmo (Suecia); los resultados del análisis de LHCb apuntan a una desviación respecto a la predicción del modelo estándar de 4,5 sigmas.” Se han observado varias “desviaciones que muestran un patrón coherente que permite identificar su origen en una única fuente. Hay que ser prudentes, porque serán necesarios más estudios teóricos y más medidas experimentales para confirmarlo. Uno de los modelos de nueva física que podría explicar estos resultados sería el que postula la existencia de una nueva partícula llamada Zprima, pero podría haber muchos otros modelos compatibles.”

Lo primero, las fuentes. El artículo teórico es Sebastien Descotes-Genon, Joaquim Matias, Javier Virto, “Understanding the B→K*μ+μ- anomaly,” arXiv:1307.5683; la charla que presenta el nuevo resultado es Nicola Serra (LHCb collab.), “Studies of electroweak penguin transitions of b→sμμ,” EPS-HEP Conference, Stockholm, July 2013 [slides]; discute el resultado el propio Joaquim Matias, “Optimizing the basis of B→K* l+l- observables and understanding its tensions,” EPS-HEP Conference, Stockholm, July 2013 [slides]. Un poco de crítica en la blogosfera en Tommaso Dorigo, “A four-sigma evidence of new physics in rare B decays found by LHCb, and its interpretation,” A Quantum Diaries Survivor, July 24, 2013, y en Lubos Motl, “LHCb: 3- or 4-sigma excess of B-mesons’ muon decays,” The Reference Frame, Jul 25, 2013.

Los datos de ATLAS, CMS y LHCb indican que las desintegraciones de los mesones B se comportan como predice el modelo estándar. Sin embargo, en el análisis de un canal concreto de desintegración se pueden introducir múltiples parámetros (observables). Las reglas básicas de la estadística dicen que si se introducen muchos parámetros aparecerán desviaciones (en unos parámetros por exceso y en otros por defecto) incluso cuando el resultado combinado se ajuste muy bien a los datos.

En la desintegración a cuatro cuerpos B→K*μμ, con K*→Kπ, se puede introducir una plétora de observables (la palabra “plétora” no es una exageración mía, aparece en la primera frase del artículo arXiv:1307.5683). Sin entrar en detalles técnicos, Descotes-Genon, Matias y Virto introducen 8 observables llamados P1, P2, P4′, P5′, P6′, P8′, AFB y dΓ/dq² (de hecho, hay muchas otras posibilidades, como usar P3 en lugar de P8′, con más y con menos parámetros). Al analizar estos parámetros por separado con 1/fb datos de colisiones a 7 TeV c.m. obtenidas en 2011 en el experimento LHCb (en ATLAS y CMS es muy difícil hacer este análisis), algunos de ellos muestran grandes desviaciones respecto a las predicciones del modelo estándar (de hasta 4,5 sigmas locales). Todavía es pronto para gritar a los cuatro vientos el descubrimiento de “nueva física” y habrá que confirmar estas desviaciones con el análisis de los 2 /fb de datos de colisiones a 8 TeV c.m. obtenidas en 2012 en el experimento LHCb. Aún resultando pesado, quiero destacar que unas desviaciones son por exceso y otras son por defecto, pero se compensan y el resultado combinado es consistente con el modelo estándar.

¿Qué valor tiene un análisis por separado de ocho parámetros de una desintegración consistente con el modelo estándar? En opinión de Descotes-Genon et al., una primera señal de “nueva física” más allá del modelo estándar podría estar oculta en las desviaciones de varios parámetros si muestran un cierto patrón regular y no son debidas al azar. Estas desviaciones de varios parámetros consistentes entre sí podrían mostrar una primera señal de “nueva física” incluso cuando está oculta en el análisis combinado de la desintegración. Por supuesto, una desviación de un sólo parámetro no es suficiente, de hecho, si fuera muy grande, el resultado combinado debería mostrar dicha desviación. Lo importante es que “haya desviaciones que muestran un patrón coherente que permite identificar su origen en una única fuente.”

¿Qué desviaciones se han observado en LHCb? No hay desviación en P1 y P4′ (aunque tienen mucho error experimental) y hay desviaciones muy pequeñas en P6′ y P8′ respecto al modelo estándar. Hay una desviación por defecto en P2 con 2,9 y 1,7 sigmas en los bins segundo y tercero, resp., que viene acompañada de una desviación en AFB. Lo más llamativo (motivo de la noticia en muchos medios) es una gran desviación por exceso en P5′ con 4,0 y 1,6 sigmas en los bins tercero y segundo, resp. (ver la parte izquierda de la figura que abre esta entrada). En general todas estas desviaciones se pueden entender como que alguno de los dos parámetros de “nueva física” llamados δC7 y δC9 sea negativo (o que lo sean los dos), en lugar de ser nulos (como predice el modelo estándar); en concreto, el mejor ajuste a 1 sigma requiere δC7∈[-0,04, -0,01] y δC9∈[-1,2, -0,5].

En resumen, conforme se acumulen datos en los experimentos del LHC la búsqueda de “nueva física” se hará mucho más refinada y los análisis multiparamétricos serán bastante habituales, pero por ahora hay pocas colisiones analizadas, la señal observada es poco confiable y la interpretación del nuevo resultado que aparece en muchas noticias está sesgada por el intenso deseo de encontrar señales de “nueva física” hasta debajo de las piedras en las que está apoyado el LHC.

Por supuesto, cuando se analice estos parámetros con los 3 /fb de colisiones en LHCb acumuladas en 2011 y 2012, podrás leer una nueva entrada en este blog sobre este asunto. Espero equivocarme, pero creo que algunas de estas desviaciones desaparecerán.

El experimento PAMELA, instalado en un satélite, ha medido el flujo de positrones en los rayos cósmicos con energía de hasta 300 GeV. Durante el mínimo del último ciclo solar entre julio de 2006 y diciembre de 2009 se han observado 24.500 positrones, muchos más de los esperados. Este exceso apunta a una fuente astrofísica (quizás galáctica) que aún se desconoce. ¿Será la materia oscura? Por ahora nadie lo sabe, pero todo apunta a otra fuente exótica. El exceso también ha sido observado por AMS-02, en la Estación Espacial Internacional, cuyos datos tienen menor error pero casi coinciden con los nuevos datos publicados por PAMELA. ¿Qué será esa fuente exótica de positrones? Quizás habrá que esperar al telescopio espacial James Webb para descubrir la fuente galáctica de tipo astrofísico responsable de este exceso de positrones. El nuevo artículo técnico es PAMELA Collaboration, “The cosmic-ray positron energy spectrum measured by PAMELA,” arXiv:1308.0133, Subm. 1 Aug 2013.

PAMELA (a Payload for Antimatter Matter Exploration and Lightnuclei Astrophysics) ha medido la fracción entre el flujo de positrones, y el flujo de electrones y positrones, φ(e+) / (φ(e+)+φ(e−)), con energía entre 1,5 y 100 GeV, en los rayos cósmicos que inciden en la tierra. En 2008 ya se publicó la existencia del exceso en los datos de PAMELA [ver aquí y aquí también], que AMS-02 ha confirmado este mismo año [ver aquí y aquí también]. Como muestra esta figura, a comparar los resultados de PAMELA con los de AMS-02 se observa que a baja energía (por debajo de 5 GeV) los resultados de PAMELA son un poco mayores que los AMS-02 (y ambos más bajos que los de otros experimentos, salvo Aesop). La razón es la dinámica del ciclo solar que modula el flujo de partículas de carga positiva en los rayos cósmicos (de origen solar, porque como ya sabrás los rayos cósmicos no tienen por qué tener un origen cosmológico). PAMELA ha tomado datos entre 2006 y 2009, cuando AMS-02 los ha tomado entre 2011 y 2013 (y otros experimentos en otros momentos del ciclo solar).

El gran problema con este exceso de positrones es que no viene acompañado de un exceso de protones. Por ello, si el origen de este exceso es la materia oscura, debe ser muy exótica, como neutralinos de muy alta masa que se desintegran con preferencia en leptones (lo que requiere un ajuste fino en los modelos supersimétricos, en contra de la “naturalidad” de la SUSY). Lo más razonable es que su fuente sea astrofísica; positrones originados en púlsares distribuidos en el halo galáctico que son acelerados por los campos magnéticos de la galaxia [ver aquí, aquí y aquí también]. El problema es que estas fuentes astrofísicas no han sido observadas aún (aunque su existencia no contradice los resultados de los modelos de simulación galáctica). Los próximos años serán muy apasionantes en este campo.

IceCube, el telescopio de rayos cósmicos situado en el Polo Sur, ha recolectado 150 mil millones de sucesos producidos por muones con energía por encima de 10 TeV. Esta ingente cantidad de datos permite estudiar anisotropías al nivel de una parte en cien mil. El resultado es que la “polaridad” de la anisotropía dipolar cambia alrededor de los 100 TeV; IceTop confirma este cambio hasta los 2 PeV. Todo apunta a dos fuentes diferentes de muones, una para los de energía por debajo de 100 TeV y otra para los de energía por encima. Un misterio más a añadir a lista de problemas sin resolver que nos muestra el universo a altas energías. El artículo técnico es IceCube Collaboration, “Observation of TeV-PeV cosmic ray anisotropy with IceCube, IceTop and AMANDA,” arXiv:1308.0246, Subm. 1 Aug 2013.

El físico de origen español Luis W. Alvarez le sugirió en 1967 al físico Gerald (Gerry) R. Lynch que modificara su simulador de Montecarlo llamado GAME para generar histogramas que incluyeran falsos “picos” (bumps) de nuevas partículas (resonancias). Los resultados del nuevo programa fueron mostrados a físicos de partículas para que indicaran “a ojo de buen cubero” si había o no había “nuevas partículas” en dichos histogramas. Muchos físicos vieron nuevas partículas donde sólo había fluctuaciones estadísticas. Nos lo cuenta Luis W. Alvarez, “Recent developments in particle physics,” pp. 1-49 en “Evolution of Particle Physics,” Academic Press, 1970. Por cierto, esta entrada viene a colación por Tommaso Dorigo, “Demystifying The Five-Sigma Criterion,” AQDS, August 11th, 2013.

En aquella época se producían entre 10.000 y 20.000 histogramas al año, que eran explorados por unos 1000 físicos a la caza de nuevas partículas. Desde 1957, los nuevos descubrimientos eran publicados en el listado del Particle Data Group (PDG). La mayoría eran hadrones (entonces no se sabía que eran partículas compuestas de quarks, aunque se sospechaba), llamados resonancias. Muchos “descubrimientos” fueron refutados por otros experimentos, por lo que se decidió marcar todas las nuevas resonancias como “no confirmadas.” Había que decidir un criterio estadístico riguroso. Arthur H. Rosenfeld, uno de los padres de la iniciativa del PDG, en una conferencia sobre mesones celebrada en 1967 en Filadelfia, usó el resultado de Gerry Lynch para proponer un mínimo de tres desviaciones típicas (popularmente llamadas sigmas) para que una “nueva” partícula fuera incorporada al PDG. Nos lo cuenta en ”The Particle Data Group: Growth and Operations-Eighteen Years of Particle Physics,” Annual Review of Nuclear Science 25: 555-598, 1975. Su artículo original de 1968 se titula “Are There Any Far-out Mesons or Baryons?,” como nos recuerda Tommaso Dorigo, “Demystifying The Five-Sigma Criterion – Part II,” AQDS, August 14th, 2013.

Tres sigmas no son suficientes, como han mostrado muchos casos. Uno de los más famosos en los que falló la regla de las tres sigmas fue el famoso descubrimiento del quark top en 1984 en el experimento UA1, liderado por Carlo Rubbia, en el colisionador SPS en el CERN. La teoría predecía 3,5 sucesos de dicho tipo y se observaron 12 sucesos (una fluctuación de tres sigmas). Pero al acumular más datos en UA1, la fluctuación cambió de signo y el descubrimiento fue desmentido pocos meses más tarde (de hecho, UA2 tampoco observó dicha fluctuación a favor). El quark top no tenía una masa de 40 ± 10 GeV/c², y gracias a UA1 y UA2 en 1990 ya se sabía que su masa era superior a 69 GeV, más allá de su capacidad de observación.

El número de cinco sigmas se estableció para el descubrimiento del quark top en 1995. En 1994 aparecieron las primeras evidencias del quark top a tres sigmas en CDF, pero el recuerdo de la historia de 1984 y que DZERO no lo hubiera observado, hizo que se recomendaran cinco sigmas para proclamar un descubrimiento. En 1995, tanto CDF como DZERO, los dos experimentos del Tevatrón, en el Fermilab, cerca de Chicago, EEUU, observaron el quark top con cinco sigmas. Hoy sabemos que tiene una masa de 173,3 ± 0,8 GeV/c² (de hecho, el LHC es una fábrica de quarks top).

Hoy en día, un descubrimiento en física de partículas requiere que dos experimentos diferentes observen el resultado con al menos cinco sigmas, que en el caso del bosón de Higgs fueron CMS y ATLAS del LHC en el CERN. Descubrimientos realizados por un único experimento, como el caso de las seis sigmas que alcanzaron los neutrinos superlumínicos del experimento OPERA en septiembre de 2011 son considerados por la mayoría de los físicos como falsas alarmas. Sólo cuando son ratificados de forma independiente por otro experimento se puede hablar en sentido estricto de un descubrimiento. Hoy sabemos que el error de OPERA era sistemático, no estadístico, debido a un fallo.

El incremento de la estadística (número de sucesos mostrados en los histogramas) produce fluctuaciones espurias a tres sigmas de forma continua y algunas pocas pueden alcanzar sin problemas las cinco sigmas; de hecho, con la ingente estadística de sucesos del LHC en la próxima década en algunas búsquedas de sucesos muy raros (como la presencia de partículas supersimétricas de gran masa) habrá falsos anuncios si no sube a entre siete y diez sigmas como cota indicativa de un descubrimiento. En la interpretación del número de sigmas de un resultado de física de partículas la clave es el consenso entre la comunidad.

Por cierto, lo he aclarado en varias ocasiones en este blog, pero quizás convenga recordar qué son las sigmas o desviaciones típicas en la significación estadística de un resultado, concepto que se utiliza en el campo del contraste de hipótesis. En este campo se estudia la probabilidad de que los datos observados en un experimento correspondan a algo nuevo (la hipótesis a contrastar) o sean resultado de una fluctuación estadística de lo ya conocido (la llamada hipótesis nula). La teoría predice para la hipótesis nula un valor medio (μ) y una desviación típica (σ). La diferencia entre valor medio observado y μ se puede cuantificar con un número de desviaciones típicas σ, es decir, con un número de sigmas. Estas son las famosas sigmas.

Por supuesto este análisis estadístico supone que las fuentes de error en la fluctuación son muchas e independientes, lo que permite aproximarla por una distribución gaussiana. En física de partículas hay errores estadísticos, que cumplen con esta condición, y errores sistemáticos, que no tienen por qué cumplirla, por ello el contraste de hipótesis utilizado es un poco más sofisticado, pero en esencia esta es la idea. Por tanto, el número de sigmas de una observación corresponde a probabilidad de que su origen sea la hipótesis nula; una sigma (desviación estándar) corresponde a una probabilidad del 16%, tres sigmas al 0,17%, y las “mágicas” cinco sigmas a una probabilidad del 0,000027%.

PS (17 ago 2013): Como Eclectikus en los comentarios, recomiendo leer a Lubos Motl, “In defense of five standard deviations,” TRF, Aug 14, 2013.

Los ricos más ricos, los famosos más famosos y los más citados más citados. Gran parte de nuestra sociedad está movida por las modas del momento. ¿Sigue la ciencia el mismo patrón? Afirma Planck, lector de este blog, que “las matemáticas son la única actividad humana que no está sometida a modas, intereses o subjetividades de ningún tipo.” ¿Estás de acuerdo? Se ha publicado un estudio en Scientific Reports que afirma que los físicos siguen las modas y se ven atraídos por los temas candentes (hot topics). Se han analizado los códigos PACS (Physics and Astronomy Classification Scheme) de todos los artículos publicados en las revistas Physical Review de la American Physical Society (APS) entre 1976 y 2009 (en total 315.082 artículos y 900.832 enlaces entre artículo y PACS). Se ha calculado la conexión preferencial (preferential attachment), que a veces se denomina “efecto Mateo” (aunque en rigor son cosas diferentes), para medir la tendencia de un nuevo artículo a adherirse a los PACS más populares de su año de publicación. Se han observado leyes de potencia que confirman el efecto. Además, el exponente de estas leyes de potencia varía en función de los países de los autores, el número de autores, el número de afiliaciones diferentes y el número de referencias. El artículo (open access) es Tian Wei et al., “Do scientists trace hot topics?,” Scientific Reports 3: 2207, 16 Jul 2013.

Los detalles del cálculo de la conexión preferencial aparecen en la sección de métodos del artículo. Lo más curioso es que la tendencia a seguir las modas cambia entre países y que el mayor valor lo alcanza China, un país aún en desarrollo en materia de investigación científica. Por ejemplo, en el año 2008, el exponente para China, α=1,06, es mayor que el de EE.UU. con 0,74, Alemania con 0,86 e incluso Japón con 0,93. Los autores creen que la razón última es la política científica en la República Popular de China que premia en metálico a los investigadores en función del índice de impacto de las revistas en las que publican, por lo que los chinos prefieren publicar en temas candentes en los que, a priori, es más fácil publicar en revistas de alto impacto.

Otro resultado curioso es que los artículos con muchos autores, muchas afiliaciones y muchas referencias prefieren temas de actualidad. Los autores creen que la tendencia podría justificarse porque trabajar en dicho tema candente ha sido el motor de la colaboración global entre estos científicos, que han montado un equipo de trabajo conjunto en el marco de un proyecto a corto plazo sobre dicho tema.

Por supuesto, los autores se han dejado muchas cuestiones en el tintero, que tendrán que ser estudiadas en el futuro. Nos cuentan en su artículo que su objetivo a largo plazo es descubrir si hay “culturas” de investigación diferentes entre países diferentes y cuantificar cómo afecta la tradición científica en un país y en un campo en la calidad de los resultados de la investigación. El tema promete ser muy interesante.

El Ecce Mono de Borja ha atraído a miles de personas a la iglesia del Santuario de la Misericordia de esta pequeña ciudad de la provincia de Zaragoza (España), algo que nunca hubiera logrado la obra de arte de Elías García Martínez. Quizás la obra de Cecilia acabe formando parte de la exposición del MOBA (Museum Of Bad Art), el único museo del mundo dedicado a recolectar, preservar y exhibir lo más pésimo del arte. Yo diría que quienes visitan Borja para admirar la obra de Cecilia siguen la propuesta de Marcel Duchamp sobre ”el arte como puro ejercicio de la voluntad, sin necesidad estricta de formación, preparación o talento.”

¿Cuánto más contemplamos una “obra de arte” más interesante y bella nos parece? ¿Cómo influye la exposición a una obra en la preferencia estética y el juicio sobre su valor? La cuestión sobre si la exposición del “arte malo” lo puede transformar en “arte bueno” ha sido estudiada por Aaron Meskin (Universidad de Leeds, Inglaterra, RU) y varios colegas. El artículo científico concluye que la simple exposición al arte malo hace que parezca aún más malo, y además que la exposición al arte bueno junto al malo hace que el bueno parezca más bueno. Yo me permito concluir que las obras del MOBA nunca acabarán formando parte del MoMA (Museum of Modern Art). El Ecce Mono de Borja acabará en el olvido, como también lo hará el Ecce Homo de Borja cuando sea restaurado. El artículo técnico de Aaron Meskin, Mark Phelan, Margaret Moore and Matthew Kieran, “Mere Exposure to Bad Art,” Brit. J. Aesthetics, AOP Feb 28, 2013.

Los resultados del nuevo artículo contradicen la opinión formada de mucha gente gracias a estudios previos, como los de Robert Zajonc que demostraron que la exposición reiterada a un estímulo malo hace que nos parezca menos malo; aunque estudios posteriores mostraron que se alcanza un umbral a partir del cual una mayor exposición no mejora la bondad del estímulo. O los experimentos de James Cutting quien mostró a una serie de sujetos parejas de obras de grandes maestros impresionistas (Caillebotte, Cezanne, Degas, Manet, Monet, Pissarro, Renoir y Sisley) que incluían una obra muy famosa junto a otra obra menor (según expertos críticos de arte), pero del mismo artista, mismo estilo, mismo objeto y mismo periodo). En las primeras exposiciones los sujetos preferían de forma clara la obra mayor a la menor, pero tras exposiciones reiteradas su gusto por la obra menor creció.

Por supuesto, la estadística del nuevo artículo es limitada y su metodología criticable, pero a pesar de ello sus resultados me parecen curiosos. Permíteme aclarar un poco los experimentos realizados. Se mostraron a estudiantes universitarios de diferentes carreras de letras imágenes en Powerpoint de obras del “pintor de la luz” Thomas Kinkade, cuyas obras para masas decoran las paredes de las casas de muchos de nuestros abuelos (porque eran bonitas, muy baratas y muy grandes) y obras del pintor prerrafaelita John Everett Millais. No hace falta decirlo, pero las pinturas de Kinkade fueron elegidas por lo malas que son (algunos críticos han llegado a decir que “son tan horribles que hay que verlas para creerlo” o que son “un crimen kitsch contra la estética”). Por otro lado, John Everett Millais está reconocido como uno de los grandes pintores británicos del siglo XIX, aunque al final de su vida produjo obras “comerciales” con paisajes cuya composición es similar a la obra de Kinkade; los críticos califican estas obras (muy criticadas por otros prerrafaelitas en su época) como de calidad buena, aunque no tanto como sus obras maestras.

Durante 14 horas de clase a lo largo de 7 semanas los estudiantes fueron expuestos a 13 imágenes (elegidas al azar entre 60 pinturas de Kinkade y Millais), cada una durante 2 segundos, sin título, ni ningún comentario del profesor. En la última clase se mostraron las 60 pinturas durante 6 segundos cada una y se pidió a los participantes que expresaran su agrado en una escala de Likert de 10 puntos. Tras un descanso, se volvieron a mostrar las imágenes en parejas elegidas de forma aleatoria, también durante 6 segundos cada par, pidiéndose a los participantes que seleccionaran cuál de cada pareja les gustaba más. A los grupos de control se les realizó sólo la segunda prueba, sin haber sido expuestos a la primera.

Los grupos de control prefirieron las pinturas “malas” de Kinkade a las obras “buenas” de Millais, pero menos cuando se mostraron en parejas que de forma individual. Los grupos expuestos de forma previa se decantaron por las obras “buenas” de Millais en lugar de las pinturas “malas” de Kinkade. Parece que un Kinkade gusta la primera vez que lo ves, pero que cuanto más lo miras menos te gusta; por el contrario, un Millais gusta menos la primera vez, pero cuanto más lo miras más acaba gustando. Si me permites un comentario personal al margen: a todo el mundo le gusta el jamón, pero cuando se prueba un buen jamón ibérico, el de bodega acaba gustando mucho menos.

Para mí lo más curioso de este estudio es que muestra que el arte también puede ser sometido al método científico (los experimentos), cada día más popular en ciencias sociales.

En el cómic “Watchmen”, el guionista inventa un mundo con superhéroes y taquiones, donde el quark strange y el charm se han descubierto en los años 50, el científico loco de turno hace experimentos para intentar encontrar los gluinos, y EEUU gana la guerra de Vietnam. Algo parecido hemos intentado hacer Mitchell Porter y yo en un hilo de PhysicsForums al que llamamos “The Wrong Turn of String Theory“, y para ello usamos varias numerologías, que he repescado aquí.

He titulado el post “Lo que pudo haber sido”, pues es como pensar en una historia alternativa de la física de partículas. Gracias a Francis por hacerme sitio para este guest post. Tenia ganas de hacer un resumen en castellano de todas estas cosas, y mi blog personal tiende a fragmentarse demasiado. No sé si necesito presentarme; ahora me dedico a cuestiones de redes sociales y asuntos informáticos, hace veinte años estudié física en la Universidad de Zaragoza y muchas de las cosas que he ido pensando -y arxivando- las podéis ver en mi página personal allí.

Sí, este post va de numerología. Dicho con más politesse, va de pistas que no tienen más fundamento que la mera numerología. Ya esta dicho. Veamos que tal sale. Si es demasiado denso o me salto cosas, siempre tenemos los comentarios.

1: Contando Partículas, o Numerología de Enteros

El primer gran tema es 128 = 84 + 44.

Hay un montón de papers de verdad, publicados y todo, sobre esta suma. El 128 es el número de componentes de un campo fermiónico en dimensión D=11 (Minkowski, uséase 10 espaciales + 1 temporal). [Aclaración: Alejandro se refiere al gravitino, un fermión de espín 3/2 asociado al gravitón, de espín 2; en D=11 hay fermiones de menos componentes, como los gauginos de espín 1/2 asociados a los bosones gauge; como aclara Alejandro en los comentarios, "cuando se compactifica a dimensiones más bajas, según cual sea la topología del espacio de compactificación, el gravitino se va descomponiendo en objetos tanto de espin 1/2 como de espin 3/2]. El 44 son las componentes del gravitón en D=11. Parece obvio que 128 no es igual a 44, así que la supergravedad se pega un tiro en el pie si insiste en tener igual número de componentes bosónicas que fermiónicas, ¿no?. Pues bueno, se salva porque llega al rescate un campo bosónico extra, un tensor antisimétrico de tres índices, que en D=11 tiene, justo, 84 componentes. ¿Qué significado tiene este campo? Una forma de verlo sería tirar del concepto de “central charges“, y que al colapsar esta supergravedad desde D=11 a D=4 apareciera una carga central con estas componentes. Otra forma, más entretenida, es mirar cuál es la fuente de la famosa membrana (2-brana) de D=11, y resulta que sí, que tanto ésta como su dual, la 5-brana, tienen su fuente en un campo de este tipo.

La construcción es super-elegante, y ahora solo bastaría tirar para abajo en el número de dimensiones usando Kaluza-Klein. Lo cual tiene su truquillo, porque bajo la alfombra de las dimensiones compactificadas se pueden sacar y meter los grados de libertad que queramos. Pero ingenuamente podríamos pensar que si tenemos 128 componentes bosónicas y 128 componentes fermiónicas, algo parecido vamos a tener en D=4.

¿Y qué es lo que tenemos hasta ahora? Bueno, pues depende de los neutrinos. En este post voy a suponer que el mecanismo que da masa a los neutrinos añade las componentes “derechas”, de forma que puede haber simultáneamente masa de Majorana y de Weyl. Lo típico de jugar al balancín (seesaw). Asumiendo estos neutrinos, llevamos observado:

1) Un gravitón, con dos componentes.

2) Un montón de fermiones, a cuatro componentes cada uno, sumando 96 componentes. Aquí me llama la atención que 96=84+12. Si miramos a las masas de los fermiones, tenemos que los de masa extremadamente pequeña, los tres neutrinos, suman 12 componentes. Pero también los de masa extremadamente grande, los tres colores del quark top, suman 12 componentes. Parece que tendríamos que tener una simetría que protege a los fermiones de saltar el balancín, y protegería a 84 de ellos, y otra simetría que debe protegerlos de adquirir una masa de escala electrodébil, y protegería a otros 84. ¿Es este el destino último de la 2-brana y la 5-brana?

3) Los bosones, a saber: El campo SU(3), con sus 8 gluones de espín 1, suma 16 componentes. El campo SU(2)xU(1), sin masa, tendría 8 componentes y el campo de Higgs, sin ruptura, cuatro. De ellas, al romperse la simetría, tres pasan a formar parte de W⁺, W⁻ y Z, así que quedan por un lado 11 componentes en SU(2)xU(1) y por el otro el famoso bosón de Higgs, con una sola. En cualquier caso, suman 16+11+1= 28 componentes. Medio coincidentalmente, el grupo de isometrías de la 7-esfera tiene 28 componentes.

Total: 96 componentes fermiónicas, 30 componentes bosónicas. Eso es lo que los experimentales han encontrado hasta ahora. En total 126 componentes.

La cuenta la revisé hace muy poco en Twitter con Amarashiki, que andaba contando partículas, pero en su origen se debe a una observación de mi antiguo director de tesis, L. J. Boya, que en algún sitio comenta que el MSSM tiene 128+128 componentes. Por cierto que LJ tiene bastantes artículos de interés para los que gustan de E8 y de teoria de representaciones. (Full disclosure: en mis tiempos nos dedicamos a Susy Quantum Mechanics, así que no soy un experto en estos temas, no los he trabajado más allá de conversaciones de seminario).

El MSSM es una lata pero, en general, ¿qué ocurre si activamos el requisito de supersimetría? Pues algo curioso con los bosones gauge masivos: como tienen 3 componentes, se les tiene que pegar por lo menos un fermión de 4 componentes, o dos de Weyl, y eso significa que necesitan una partícula extra en el lado bosonico. El supermultiplete del Z⁰ se puede completar con el bosón de Higgs que acaba de descubrir el CERN, pero los del W⁺ y W⁻ necesitan otros dos bosones. Los que hayais leido hasta aquí, haced un poco de “hep-ex-fiction” y asumid que en la siguiente ronda del LHC aparece un H⁺ (y un H⁻). Tendríamos un catálogo de 96 componentes fermiónicas y 32 componentes bosónicas, que incluirían el gravitón y estas dos “por descubrir”. Visto de otro modo, si a las 96 componentes fermiónicas descubiertas les pudiéramos sumar los 32 partners, usease gluinos (16), winos (8), zino (4), fotino (2) y gravitino (2), sumarían 128 componentes. Justo las que necesita un fermión de D=11. Así que el amigo Alan Moore estaba bastante inspirado cuando ponía al Dr Manhattan a buscar esos gluinos. Pero incluso si no se encuentran, no deja de ser curioso que estamos a punto de agotar la física de partículas quedándonos justo con la mitad de las partículas que uno esperaría haber encontrado en SuperGravedad. Bueno, casi la mitad, a falta de ese bosón cargado.

¿Y en dirección inversa, no tendríamos que buscar también los 96 escalares que acompañan a los fermiones del modelo estándar? Pues mira, aquí es donde yo iba camino de Damasco y se me tropezó el caballo y oí una voz que me decía… bueno, no, pero algo así. Resulta que estaba un poco mosca intentando entender por qué el señor Koide habia empleado relaciones que parecían (y sólo parecían) reglas de masas para mesones, y le di vueltas a lo de que el muón tiene más o menos la misma masa que el pión y que, nueva coincidencia numerológica, conocemos seis mesones cargados de espín cero. Justo lo que necesitamos… Mirando con más detalle, resulta que el espectro de “cuerdas abiertas orientadas” de QCD proporciona estos 96 escalares si no dejamos que el quark Top aparezca en los extremos de esta cuerda.

Dicho de otra forma, en lenguaje de grupos: la parte escalar de supersimetría parece tener una simetría global SU(5) que se descompone en SU(3)xSU(2) con asignación de carga eléctrica y de color similar a los 3 quarks dsb y a los dos quarks uc. El producto de una representacion 5 y una anti-5 de SU(5) se descompone en 24 + 1 y esos 24 son justo los 12 sleptones cargados y los 12 sneutrinos. El producto de una representación 5 por otra 5 se descompone en 15 + 10, y ese 15 contiene los 12 antiquarks de un color dado. Esto lo he contado por el arxiv de cuando en cuando, y también en el blog viejo de Dorigo.

Así pues, puede que todo lo que quede de los sfermiones sea el espectro de mesones y diquarks. No hay un modelo dinámico directo, y la cuerda abierta orientada esta prohibida en superstrings. Pero la cuenta de escalares coincide, carga a carga, con la que necesitamos. Ah, y está claro que el truco sólo funciona bien con tres generaciones y un quark top que sea mucho más pesado que QCD, para que no forme mesones y salgan las cuentas. Pocos modelos hay que exijan un mínimo de tres generaciones.

Por cierto, a ver si algún día alguien me explica a quién se le ocurrió llamar “sfermión” a un escalar, que es partícula de Bose.

Intermedio: bajando dimensiones

Volvamos un momento a lo de que nos han salido 28 componentes en el sector bosónico del modelo estándar. Visto como partículas, son 8 portadores de fuerza fuerte, 4 portadores de electrodébil, y un campo de Higgs en doblete. En realidad no pueden ser un subgrupo de SO(8); pero la conexión con la 7-esfera es un falso camino, por mucho que sea el camino que se exploró en la mayoría de los modelos, generalizando a partir de otros que se habían hecho para jugar con Kaluza-Klein en la 3-esfera.

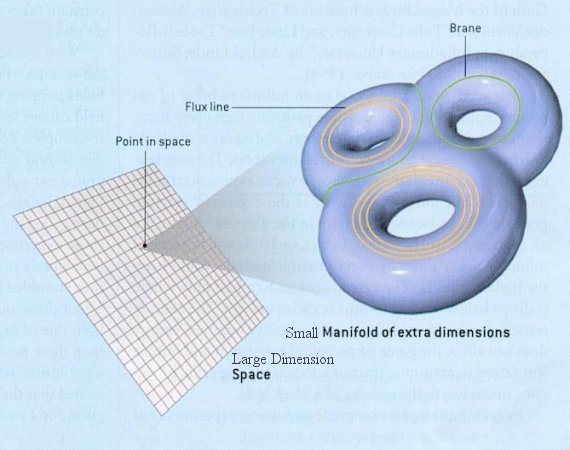
A Witten se le ocurrió otro modelo. Debió pensar en Pati-Salam, SU(4)xSU(2)xSU(2), y jugando a que SU(4) es como SO(6) y a que SU(2)xSU(2) es como SO(4), parece obvio que Pati-Salam es el grupo de simetrías (de isometrías) de la variedad producto de la 5-esfera y la 3-esfera. Esta es una variedad de dimensión 8. Haciendo su cociente arbitrario por cualquier recorrido del grupo U(1), el amigo Edward se dio cuenta de que la resultante iba a ser de dimensión 7 y que su grupo de isometrías sería en general SU(3)xSU(2)xU(1). Esto es, Kaluza-Klein en D=11 prácticamente implica que cuando cocientemos a D=4 nos van a salir de regalo, si buscamos hacerlo de forma no trivial, los mismos grupos que tiene el modelo estándar. Pero estas variedades compactificadas no son esferas, que al tener la máxima simetría posible sería lo más elegante. Son justo su mitad, en un sentido: la esfera es la fibración de S³ sobre S⁴, y estas variedades son fibración de S³ sobre CP². En algún sitio cuenta Atiyah de qué manera CP² y S⁴ son una la mitad de otra: “branched covering“.

Es bastante interesante que haya que jugar con el modelo de Pati-Salam, sacándolo de un espacio compacto desde D=12. La gente de cuerdas tiene algunos casos en los que trepa a esta dimensión pero tiene que poner signaturas exóticas, 10+2 y cosas así. No se puede hacer una SUGRA decente más allá de D=11, pero parece que hay que visitar esa tierra. Puede que tenga que ver con que Pati-Salam necesita, al romperse, tener un campo que no es un campo gauge, el U(1) correspondiente a la simetría B-L. El espacio de D=12 válido sería el producto directo de una de las variedades de Witten por un U(1), y este grupo daría cuenta de la carga B-L. También Connes en sus modelos encuentra natural usar Pati-Salam primero y luego cocientar. Y hasta Baez y Huerta lo usan en su cuadrado para bajar desde SO(10) al modelo estándar.

El abandono de Kaluza-Klein fue, en mi opinión, otro accidente histórico. La revolución de turno en las supercuerdas dejó desmantelado el campo. Y Francis se pregunta si los cientificos siguen modas.

2: Poniendo Masas, o Numerología de Escalas.

He hablado de Koide, y es un tema que suele salir en comentarios, así que vamos a ello. ¿Me ha servido la visita al mundo de los números enteros y de las teorías de grupos y supercosas, conversión a cuerdas (open strings) incluida, para entender algo de las masas? Pues de momento no, pero tampoco me descuadra. Ya he dicho que me asombra la coincidencia entre masas de QCD (como el pión) y masas del modelo estandar (como el muón). Aproximando un poco aquí y allá, me atrevo a ponerlas todas juntas en seis niveles:

donde he completado cada nivel para que tenga dos partículas, a base de añadir los neutrinos con lo que sospecho sería su masa antes del see-saw. Creo que tenemos aquí un desdoblamiento o ruptura parcial de Pati-Salam, con leptones y quarks todavía alineados por SU(4), y que podemos plegarlo de nuevo, quedándonos en tres “generaciones”:

de forma que todas las relaciones de Koide que conocemos unen una partícula de cada nivel: por supuesto la original (e,mu,tau) pero tambien los demás de la “Koide Waterfall“: (s,c,b), (c,b,t) y (u,s,c) y (d,u,s). Cada uno de estos tripletes cumple la ecuación de Koide, aunque podemos argüir que no tiene demasiado mérito dado que sólo el Top tiene una masa medible. Y de alguna manera, la relación de Koide sobrevive al desdoblamiento.

La ecuacion de Koide de un triplete dado es con las condiciones y . Por tanto . Aquí hay una coincidencia muy llamativa, de las de numerología de escalas de energía. Resulta que

la masa correspondiente al triplete de leptones es igual a la masa del quark de QCD. Si ya no había ninguna razón para que el muón y el pión tuvieran masas cercanas, esto es una incógnita mayor, pero ahí esta. Ahora, resulta que es posible encajar las masas de s,c,b usando una masa que sea el triple de la de los leptones. Esto es, 941.4 MeV, aunque no hay por que preocuparse del valor concreto, simplemente lo curioso es que basta un factor tres para que encajen un triplete de leptones y uno de quarks. Y una vez encajadas s,c,b podemos predecir la masa del top volviendo a aplicar Koide sobre c,b,t. El resultado: 173.26 GeV.

Es posible que algunos de vosotros hubierais leído en su día la critica de Lubos sobre la ecuación de Koide. Lamentablemente, Motl tiende a ignorar los preprints que considera una pérdida de tiempo, y eso suele incluir los míos. Así que en su crítica desconocía los resultados para quarks. Y seguramente no habría ni siquiera tomado en cuenta las masas de niveles similares a QCD, dado que la ideología dominante es que todos los valores de las masas descienden desde los valores de los acoplos de Yukawa en la escala de Planck, sin ninguna condición especial a la escala de QCD.

Pero visto desde abajo, resulta que la cuerda de QCD tiene la escala de masas necesaria para Koide y los sabores necesarios para imitar supersimetría con tres generaciones. Puede que la supercuerda de 1971, la de los modelos duales de quarks y gluones, fuera después de todo el modelo correcto.

Diferencia entre los datos de Planck y WMAP-9 para el fondo cósmico de microondas. Fuente: arXiv:1305.4033

Nadie sabe el porqué, pero hay una diferencia mayor de la esperada entre el fondo cósmico de microondas (CMB) observado por Planck (publicado por ESA en marzo de 2013) y por WMAP-9 (publicado por NASA en diciembre de 2012). Suponiendo que los datos de Planck son más fiables, los datos de WMAP-9 presentan un dipolo cuyo origen es desconocido, pero se cree que debe ser resultado de algún tipo de contaminación. De hecho, comparando los datos de WMAP-9 y WMAP-7 también se observa dicho dipolo, aunque con menor amplitud. La comparación se ha realizado filtrando los datos de Planck para que su resolución coincida con la de WMAP-9. La diferencia entre ambos es la responsable de que según Planck haya más materia oscura y menos energía oscura en el universo de lo que indicó WMAP-9. Más información técnica en Anne Mette Frejsel, Martin Hansen, Hao Liu, “Consistency tests for Planck and WMAP in the low multipole domain,” arXiv:1305.4033, 17 May 2013, y en András Kovács, Julien Carron, István Szapudi, “On the Coherence of WMAP and Planck Temperature Maps,” arXiv:1307.1111, 03 Jul 2013.

Esta figura muestra la diferencia entre WMAP-9 y WMAP-7 (recuerda que son los datos del CMB observados por WMAP tras 9 años y tras 7 años de observación). La diferencia tiene una amplitud máxima de 0,01 mK, cuando entre Planck y WMAP-9 la diferencia alcanza los 0,03 mK. Aún así, la presencia de este dipolo es sospechosa y podría ser indicativo de que existe algún tipo de contaminación en los datos de WMAP-9 que ha sesgado nuestro conocimiento sobre el contenido del universo.

Comparando los datos de WMAP-9 con los de Planck asumiendo la validez del modelo de consenso ΛCDM se observa una diferencia al nivel de 3 σ, que desaparece si se multiplica la señal de WMAP-9 por un factor de 1/1,024 = 0,976 (la diferencia entre el primer pico acústico observado por ambos experimentos). Este resultado es curioso y apunta a algún error sistemático en las medidas de WMAP-9, pues todo el mundo asume que las de Planck son mucho más precisas. Sin embargo, no todo el mundo está de acuerdo con esta interpretación. Si se tiene en cuenta la variación cuadrática de esta amplitud la discrepancia se reduce a sólo 1 σ, lo que indica que ambos resultados son consistentes entre sí, como nos muestran Dhiraj Kumar Hazra y Arman Shafieloo, “Test of Consistency between Planck and WMAP,” arXiv:1308.2911, 13 Aug 2013.

Estos físicos coreanos han supuesto una variación cuadrática de la amplitud del primer pico acústico (han usado un polinomio en la base de Chebyshev con tres coeficientes C0, C1 y C2, en los que C0 corresponde a la variación en la amplitud del pico). Suponiendo fija la amplitud del pico (C0=1) se observa la discrepancia a 3 sigmas, como se muestra en la gráfica de arriba de esta figura. Sin embargo, permitiendo una variación de los tres coeficientes (C0 variable) la discrepancia se reduce a 1 sigma, como se muestra en la gráfica de abajo de esta figura. En estos ajustes se ha tomado el modelo de consenso ΛCDM de Planck como “exacto” y se ha utilizado para ajustar los valores de C1 y C2 usando los datos observados de Planck (en verde en las figuras) y WMAP-9 (en azul).

Como es obvio, este tipo de análisis no resuelve la cuestión de fondo. Hay una mayor diferencia entre WMAP-9 y Planck de la esperada y ahora mismo hay grupos de investigación de ambas colaboraciones que están tratando de descubrir el porqué.

Una kilonova es el resultado de la fusión de dos estrellas de neutrones o de una estrella de neutrones y un agujero negro; se trata de un evento astrofísico similar a una supernova débil de vida muy corta. El telescopio espacial Hubble de la NASA ha observado una posible kilonova en el brote de rayos gamma GRB 130603B tanto en el óptico como en el infrarrojo. La primera observación de un fenómeno predicho por la teoría siempre está acompañada de dudas, por lo que habrá que esperar a futuras observaciones para confirmar esta kilonova (por cierto, en algunos sitios la llaman macronova o supernova de proceso-r, donde “r” proviene de rápido). Lo más interesante de las kilonovas es que producen una señal de ondas gravitatorias que podría ser observada por la nueva generación de detectores por interferometría. El artículo técnico es N. R. Tanvir, A. J. Levan, A. S. Fruchter, J. Hjorth, R. A. Hounsell, K. Wiersema & R. L. Tunnicliffe, “A ‘kilonova’ associated with the short-duration γ-ray burst GRB 130603B,” Nature, AOP 03 August 2013.

El verano es la época ideal para conversar. En los últimos días Amarashiki (@riemannium,TSOR), Alejandro Rivero (@arivero,web) y Kac-Moody (@1KacMoody1) han mantenido una interesante charla sobre la supergravedad (Sugra) y las teorías de Kaluza-Klein (KK) en Twitter sobre la cuestión “¿por qué se abandonó la línea de investigación en [teorías de Kaluza-Klein y Sugra] en 1985?,” que surgió al hilo de la entrada de Alejandro como invitado en mi blog (“Lo que pudo haber sido“). No soy experto en estas lides, pero yo creía que la razón estaba bastante clara: la primera revolución de la teoría de supercuerdas en el verano de 1984 y los problemas que antes de dicho verano se habían detectado en las teorías de supergravedad en 11 dimensiones relacionados con la quiralidad del modelo estándar y con sus divergencias ultravioletas (se trata de una teoría no renormalizable). Para los expertos en Kaluza-Klein y supergravedad cambiar de tópico de trabajo a la teoría de supercuerdas prometía muchos más éxitos. Por todo ello creo que fueron abandonadas estas ideas. Como sus problemas aún no han sido resueltos y se cree que no tienen una solución elegante, siguen abandonadas. Permíteme recordar la situación de las teorías de Kaluza-Klein y de supergravedad antes del verano de 1984 (me basaré, como no, en M.J. Duff, B.E.W. Nilsson, C.N. Pope, “Kaluza-Klein Supergravity,” Physics Reports 130: 1-142, 1986, y en M.J. Duff, “Supergravity, Kaluza-Klein and superstrings,” pp. 18-60 en 11th Intl. Conf. General Relativity and Gravitation, Cambridge UP, 1987).

Los físicos creemos que la realidad está formada por dos entidades básicas: espaciotiempo curvado (la gravedad) y campos cuánticos (el modelo estándar). Hay dos caminos posibles para una “teoría de todo” que unifique ambas entidades en la escala de Planck. El primero es que todo es espaciotiempo curvado y por tanto los campos (cuánticos) son el resultado de la existencia de dimensiones extra del espaciotiempo muy curvadas y de forma muy compacta. Copar con campos clásicos es fácil y esta es la idea de las teorías de Kaluza-Klein y de la supergravedad; sin embago, en el caso cuántico hay un grave problema, esta teoría no es renormalizable, como tampoco lo es la versión cuántica de la gravedad de Einstein, y por tanto no puede ser válida en la escala de Planck.

Y el segundo camino es que todo son campos cuánticos y el espaciotiempo es una entidad emergente, aunque por el momento no tenemos muy claro cómo emerge. Hay muchas propuestas en diferentes grados de desarrollo. La más popular y la que presenta un mayor grado de evolución es la asociada a campos cuánticos “cuerdísticos” (la generalización de los campos de partículas “puntuales” a campos de cuerdas y branas), en la llamada teoría de cuerdas y teoría M (ST/MT). Gracias a la simetría del espejo (“mirror symmetry”) y a la dualidad T se sabe que en esta teoría no existen las distancias menores que la longitud de Planck, aunque la descripción detallada de la teoría a esta escala no es conocida en detalle. Sin embargo, hay muchas otras ideas para entender la emergencia del espaciotiempo; sin ser exhaustivo me vienen a la cabeza las siguientes posibilidades (todas en un grado de desarrollo que podemos calificar como “pobre” comparado con ST/MT y cuya consistencia interna está sujera a grandes dificultades técnicas aún no resueltas): las ideas asociadas a la gravedad cuántica de bucles (LQG), las ideas asociadas al principio holográfico, las asociadas a la causalidad de las interacciones entre campos como la teoría de triangulaciones dinámicas causales (CDT), y las asociadas a fuerzas entrópicas entre los campos como en la teoría de la gravedad entrópica de Erik Verlinde. Para evitar malentendidos, me gustaría recalcar que la única teoría de gravedad cuántica consistente hasta el momento es la ST/MT y que en la actualidad hay físicos tratando de incorporar las demás ideas en el marco ST/MT con objeto de transformarlas en teorías consistentes.

Volvamos a la idea de Kaluza-Klein, impecable a nivel clásico. Las ecuaciones de la gravedad de Einstein para un espaciotiempo con D>4 dimensiones describen además del gravitón (partícula de espín 2), bosones gauge (partículas de espín 1 descritas por ecuaciones de Yang-Mills) y bosones escalares llamados dilatones (de espín cero que se puede hacer que actúen como bosones de Higgs). La topología de las D – 4 dimensiones extra es diferente del resto, son compactas (cerradas y acotadas, como una esfera o un toroide), por lo que tienen un tamaño finito. Las simetrías del modelo estándar, SU(3)xSU(2)xU(1), se pueden incorporar tomando un grupo G de simetría que contenga a SU(3)xSU(2)xU(1) y compactificando las dimensiones extra con una variedad diferenciable cuyo grupo de isometría sea G (a este idea se le suele llamar graviGUT, porque el grupo G define una teoría de gran unificación o GUT).

¿Por qué no observamos las D – 4 dimensiones extra del espaciotiempo? En las teorías de Kaluza-Klein las cargas (gauge) son proporcionales a la constante de Newton de la gravedad y el factor es una función inversa al tamaño de las dimensiones extra; como las cargas gauge son muy grandes comparadas con la gravedad, recuerda que es muy débil, las dimensiones extra tienen un tamaño muy pequeño. Lo habitual es tomar la escala de Planck (unos 10^-33 cm). La versión cuántica de la teoría implica la existencia de nuevas partículas asociadas a campos confinados en las dimensiones extra campactas, llamadas partículas de Kaluza-Klein; no observamos estas partículas porque su masa es del orden de la energía de Planck (unos 10¹⁹ GeV).

Las teorías de Kaluza-Klein (o teorías graviGUT) tienen muchos problemas, pero mencionaré sólo tres de ellos. El primero es que la teoría no incorpora fermiones (leptones y quarks), que como en el caso del modelo estándar, han de ser introducidos ad hoc como en cualquier otra teoría GUT (luego no se trata de una teoría de todo, sino de “casi todo”). El segundo es que la versión cuántica de estas teorías no es renormalizable (los problemas que aparecen al cuantizar la gravedad de Einstein en 4 dimensiones se mantienen en D dimensiones). Y el tercero que mencionaré es que la teoría no es quiral, a diferencia del modelo estándar, y no se conoce ningún mecanismo de rotura espontánea de la simetría que rompa una teoría no quiral en una teoría quiral. Que no me peguen los expertos. Se han publicado soluciones a estas problemas, pero no son del todo satisfactorias. Por ejemplo, en lugar de usar las ecuaciones de Einstein para la gravedad que tienen derivadas hasta el segundo orden, como las ecuaciones de Newton, se puede usar una generalización con infinitas derivadas cuya versión cuántica parece ser renormalizable, pero que mantiene otros problemas.

Una solución natural para incorporar fermiones en una teoría de Kaluza-Klein es utilizar la supersimetría, que conduce a la teoría llamada supergravedad. La supersimetría es una simetría que transforma fermiones en bosones y viceversa. Además, aplicar dos transformaciones supersimétricas equivale a una traslación en el espaciotiempo, es decir, la supersimetría equivale a una raíz cuadrada de una traslación (SUSY²=TRASLACIÓN). La supergravedad es la teoría tipo gauge basada en la supersimetría como simetría local y no hay que meter de forma explícita las ecuaciones de Einstein, ya que esta teoría incluye una partícula de espín 2, que actúa como gravitón, y la gravedad aparece de manera natural (algo parecido ocurre en QED al hacer la simetría U(1) local aparece el electromagnetismo como arte de magia). Asociado al gravitón hay partículas de espín 3/2 llamados gravitinos; su número es igual al número de supersimetrías diferentes de la teoría. Hay varias razones teóricas en contra de la existencia de partículas de espín mayor de 2, por lo que el número máximo de supersimetrías es N=8. Este número de supersimetrías determina el espectro completo de partículas. Por ejemplo, para N=8 supersimetrías hay un supermultiplete que contiene un gravitón (espín 2), 8 gravitinos (espín 3/2), 28 bosones vectoriales (espín 1), 56 fermiones de espín 1/2, y 70 bosones escalares (espín 0).

Una teoría de todo debe ser única (en algún sentido) y la supergravedad es única en D=11 dimensiones. La razón es que el número de supersimetrías impone un número máximo de dimensiones para el espaciotiempo. Como el número de supersimetrías es N≤8 y un espinor de Dirac en 4 dimensiones tiene 4 componentes, el número máximo de componentes permitido para un espinor de Dirac en D dimensiones debe ser 32 lo que obliga a que D≤11 (el número de componentes de un espinor de Dirac es igual a 2^(D-1)/2 para D impar y 2^D/2 para D par). El espaciotiempo tiene 4 dimensiones, luego la teoría en 11 dimensiones debe tener 7 dimensiones extra compactificadas en el sentido de las teorías de Kaluza-Klein.

La dualidad entre supergravedades (N=1 en D=11)↔(N=8 en D=4) es muy sugerente y llevó a prestar mucha atención a la (única) teoría de la supergravedad N=1 en D=11 dimensiones. La gravedad en esta teoría descrita por un tensor métrico de 44 grados de libertad (componentes del campo del gravitón) y un gravitino de 128 componentes. La supersimetría obliga a que aparezcan campos bosónicos de 84 componentes (84+44=128). Además de aparecer las ecuaciones de Einstein sin ser impuestas, también surge la separación de las dimensiones extra M₁₁=M₄xM₇, cuando el tensor de cuatro índices de intensidad del campo gauge de 84 componentes es constante (es decir, lo más simple posible). La fenomenología de la teoría N=8 en D=4 da muchos problemas y es preferible una teoría N=1 en D=4; a principios de los 1980 hubo mucho revuelo cuando se descubrió que tomando M₇=S⁷ (la esfera en 7 dimensiones) aparece de forma natural un mecanismo de Higgs que rompe la supersimetría N=8 en D=4 en la supersimetría N=1 en D=4, pero su grupo de holonomía H(M₇)=G₂ que implica un grupo gauge SO(8) que no es suficiente para contener el modelo estándar SU(3)xSU(2)xU(1). Hay otras propuestas para M₇ que permiten grupos más grandes capaces de albergar el modelo estándar, pero ninguna admite una rotura de simetría “natural” hasta N=1.

Volvamos al principio, ¿por qué se abandonó la idea de la supergravedad N=1 en D=11 tras el verano de 1984 cuando en 1983 podríamos decir que había euforia por ella? Como es obvio influyó la primera revolución de la teoría de cuerdas, la teoría de supercuerdas de 1984, pero hay razones más importantes que están descritas en todos los artículos de revisión sobre esta teoría. Destacaré tres de ellas.

La primera es un artículo de Edward Witten que mostró que una supergravedad en D=11 con dimensiones extra compactificadas en una variedad diferenciable no puede ser rota de forma espontánea a una teoría quiral en D=4 dimensiones. Si la teoría no es quiral en D=11 entonces tampoco lo puede ser en D=4 (la quiralidad se preserva en dimensiones impares y sólo puede surgir en la rotura de simetría en espaciotiempos con dimensión par). Para resolver este problema se puede “complicar” la teoría en D=11 introduciendo ad hoc la quiralidad o usando simetrías “ocultas”, pero la unicidad, la simplicidad y la belleza de la teoría desaparece. Los pocos expertos que siguieron investigando en supergravedad tras la revolución de la teoría de cuerdas se concentraron en la teoría en D=10 dimensiones. Pero los fermiones quirales tienen asociados la aparición de anomalías quirales que violan las simetrías gauge de la teoría Yang-Mills en D=4; se pensó que podrían ser eliminadas con una compactificación adecuada, pero se demostró en 1983 que dicha compactificación no existe. Para resolver este problema basta compactificar en una variedad que no sea diferenciable (como una red discreta), pero a mucha gente no le gusta esta idea porque no se puede recuperar de forma fácil el modelo estándar.

La segunda razón por la que en 1985 se relegó a un segundo plano la idea de la supergravedad N=1 en D=11 fue que la compactificación de las dimensiones extra introduce una constante cosmológica enorme, proporcional a la masa de Planck al cuadrado; en aquel momento se pensaba que la constante cosmológica era nula (hoy sabemos que existe la energía oscura, pero la constante cosmológica es unos 120 órdenes de magnitud más pequeña que la masa de Planck al cuadrado). Hoy en día se pueden reducir estos 120 órdenes de magnitud a menos de 60 (según los detalles técnicos), un número que sigue siendo enorme.

La tercera razón, quizás la más importante es que la teoría no es renormalizable y presenta divergencias ultravioletas. Ha habido progresos recientes en la renormalización de “la supergravedad N=8” (yo los califiqué en este blog de forma muy optimista como “una nueva revolución en la física teórica“), pero el problema de fondo sigue siendo el mismo. Aunque la teoría sea renormalizable hasta 5 bucles, hay argumentos fuertes en contra a partir de 7 bucles, inclusive. Hoy en día no parece que la teoría pueda ser renormalizable a todos los órdenes. La teoría de cuerdas, por el contrario, parece finita a todos los órdenes.

En resumen, espero que esta entrada aclare un poco mi opinión sobre este asunto que se discutió en Twitter y espero que en los comentarios, si os apetece, continuemos el debate, si os sigue suscitando interés.

Hace más de dos siglos que Theodor von Grotthuss propuso un mecanismo para entender el transporte de iones en el agua: su transferencia entre un catión hidronio H₃O⁺ y un anión hidróxido OH^- a través de una serie de saltos entre puentes de hidrógeno en el agua (los enlaces intermoleculares entre los hidrógenos y los oxígenos de moléculas H₂O diferentes), como si los protones se movieran por “cables” de agua (proton wires). Se publica en PNAS un artículo que aclara los detalles técnicos de este proceso mostrando la importancia de la topología de la red tridimensional de puentes de hidrógeno en el transporte y la formación de “cables” en forma de anillo. Hassanali et al. han usado simulaciones por ordenador de dinámica molecular ab initio (AIMD por Ab Initio Molecular Dynamics) que muestran que el transporte ocurre a ráfagas, con periodos de reposo en los que no hay transferencia de protones y estos están localizados (parecen atrapados); en estos periodos de reposo, cuya duración es mayor de la que se pensaba, se observan aniones hidróxido ”hipercoordinados” cuyo oxígeno tiene 4 puentes de hidrógeno simultáneos en una configuración casi plana; se cree que el transporte se activa cuando estos hidróxidos fluctúan y su número de puentes de hidrógeno se reduce de 4 a 3. El proceso presenta múltiples escalas de tiempo y es más complicado de lo que se pensaba. Por supuesto, ahora es el turno de los físicoquímicos experimentales que tendrán que confirmar estos detalles por observación directa. Nos lo han contado Edelsys Codorniu-Hernández, Peter G. Kusalik, “Probing the mechanisms of proton transfer in liquid water,” PNAS, AOP Aug 8, 2013, que se hacen eco del artículo técnico de Ali Hassanalia et al., “Proton transfer through the water gossamer,” PNAS, AOP Jul 18, 2013.

Esta figura ilustra los aniones hidróxido ”hipercoordinados” cuyo oxígeno está conectado a cuatro hidrógenos, parte (a), y los anillos que se forman entre moléculas de agua gracias a los puentes de hidrógeno sin intervención de los iones, parte (b). En los anillos que sólo contienen moléculas de agua cada molécula aporta dos átomos (un oxígeno y un hidrógeno) y forma dos enlaces de hidrógeno; a esta configuración de los átomos se la llama DA (por donante-aceptor).Estos anillos se rompen cuando una molécula de agua pasa una configuración DD (doble donante) o AA (doble aceptor); un teorema de la teoría de grafos dirigidos obliga a que un anillo cerrado con una molécula DD debe tener siempre alguna otra molécula AA (algo que no depende del número de moléculas del anillo ni de su forma concreta). Este tipo de anillos DD-AA son poco probables porque son inestables en un entorno molecular tan complicado con un “baño” de agua.

Los anillos DD-AA son claves en el transporte de protones y las simulaciones por ordenador indican que los iones hidronio e hidróxido pueden desempeñar el papel de moléculas de agua DD y AA, respectivamente, incrementando la probabilidad de aparición de estos anillos. Los hidronios actúan como “fuentes” de protones que se irradian a través de alguno de los múltiples caminos que se bifurcan a partir de su posición en los anillos. Los hidróxidos actúan como “sumidero” para los protones que reciben por algunos caminos, provocando periodos de reposo cuando dejan de estar hipercoordinados.

Los resultados muestran la gran importancia de la topología de los anillos en el transporte de protones en el agua líquida. Las múltiples escalas de tiempo que se observan son debidas a las fluctuaciones de la topología de la red de puentes de hidrógeno, conforme los anillos aparecen y desaparecen, o cambian entre configuraciones de diferente longitud. El transporte de protones de unos anillos a otros es el responsable último del fenómeno de difusión de los protones en el agua, clave en las reacciones químicas ácido-base de gran interés básico y aplicado.

La optogenética consiste en acoplar proteínas fotosensibles a otras proteínas y lograr el control de su función; hoy se usa para activar y desactivar las sinapsis de neuronas mediante pulsos de luz que actúan sobre los canales iónicos y las bombas de iones en sus membranas. Nature publica una nueva técnica optogenética para regular la expresión de genes in vivo y de forma no invasiva usando luz láser de diferentes colores; la regulación de la actividad enzimática tiene gran número de aplicaciones y la nueva técnica tiene múltiples ventajas respecto a otras técnicas anteriores. Nos lo cuentan Andreas Möglich, Peter Hegemann, “Biotechnology: Programming genomes with light,” Nature 500: 406–408, 22 Aug 2013, que se hacen eco del artículo técnico de Silvana Konermann et al., “Optical control of mammalian endogenous transcription and epigenetic states,” Nature 500: 472–476, 22 Aug 2013.

La optogenética es una rama de la bioingeniería que aprovecha los fotorreceptores de plantas y microorganismos para diseñar sistemas de control activo de proteínas. El más usado es el criptocromo 2 (CYR2), que al recibir luz azul se acopla a una proteína llamada CIB1. Lo más sencillo es acoplar esta proteína a un factor de transcripción que controle la expresión de un gen para regularlo usando luz; recuerda que un factor de transcripción es una proteína que se une a una secuencia de ADN concreta cercana a un gen concreto y facilita que la ARN polimerasa inicie la transcripción de dicho gen a ARN mensajero. Esta técnica sólo permite controlar genes muy concretos, pues los factores de transcripción son muy específicos.

Lo ideal sería poder controlar cualquier gen con un mecanismo que reconociera una secuencia de ADN cualquiera y activara la transcripción del gen más cercano. Para ello en ingeniería genética se utilizan proteínas TALE (Transcription-Activator-Like Effector) capaces de reconocer una secuencia de ADN repetitiva e introducir un corte en la doble hélice de ADN; el proceso de reparación de ADN puede ser engañado y ser utilizado para introducir nuevos elementos genéticos en el lugar del corte.

Konermann y sus colegas combinan la optogenética basada en CYR2 y la ingeniería genética basada en proteínas TALE en una nueva técnica llamada LITE (Light-Inducible Transcriptional Effector). Demuestran su técnica usando dos genes llamados Grm2 y Neurog2 en neuronas de ratón. Unos minutos después de iluminar las neuronas se observa un incremento en un factor de 10 a 20 en la expresión de estos genes, relativo a su expresión sin iluminación. La técnica LITE es reversible, ya que al eliminar la iluminación la tasa de expresión vuelve a su estado original. Aunque la técnica ha sido demostrada in vitro (con células cultivadas), nada impide que pueda ser aplicada in vivo (las técnicas optogenéticas ya han sido usadas en animales vivos).

Konermann y sus colegas han demostrado también el uso de luz de diferentes colores para controlar la expresión de diferentes genes. Para ello han aplicado LITE a varias moléculas que modifican las histonas (las proteínas en las que se enrolla el ADN en los cromosomas), controlando su metilación y acetilación (dos modificaciones epigenéticas de la transcripción). Estas y otras demostraciones de la técnica LITE muestran su gran versatilidad para activar la transcripción de genes seleccionados a medida y promete muchas aplicaciones prácticas.

En el punto triple del agua (a 0,01 °C de temperatura y 612 pascales de presión) coexisten en equilibro sus tres estados sólido, líquido y gaseoso. El dióxido de vanadio es un sólido que presenta un punto triple a 65 °C en el que coexisten tres fases sólidas, dos aislantes (con estructuras cristalinas monoclínicas, M1 y M2) y una conductora (con estructura tetragonal tipo rutilo, R). Gracias a un dispositivo micromecánico se ha medido con alta precisión el diagrama de fase temperatura versus esfuerzo en tracción de una nanobarra de dióxido de vanadio (VO₂). Películas delgadas de óxido de vanadio se utilizan mucho en la industria electrónica y en óptica física como “material inteligente” (porque sus propiedades varían mucho con la temperatura y el voltaje aplicado). La más interesante de las tres fases es M2 ya que no hay ninguna teoría microscópica que explique su estabilidad; el nuevo diagrama de fase guiará los cálculos de la estructura electrónica mediante ordenador, lo que quizás ayude a aclarar este asunto. Existen puntos triples sólidos en la manganita y en niquelatos de tierras raras, aunque aplicar el nuevo método de medida no será fácil pues se requieren nanobarras de muy alta calidad. Nos lo cuenta Douglas Natelson, “Condensed-matter physics: A solid triple point,” Nature 500: 408–409, 22 Aug 2013, que se hace eco del artículo técnico de Jae Hyung Park et al., “Measurement of a solid-state triple point at the metal–insulator transition in VO2,” Nature 500: 431–434, 22 Aug 2013.

En las tres fases del dióxido de vanadio hay dos conjuntos de cadenas paralelas de átomos de vanadio (en negro en la figura), cada uno rodeado de seis átomos de oxígeno (no mostrados en la figura) que forman un octaedro distorsionado. En la fase R (de tipo rutilo), a alta temperatura, todas las cadenas son rectas y periódicas, mientras que en la fase M1 (monoclínica) todos los átomos de vanadio forman dímeros. Hay otras dos fases aislantes; la fase M2 (monoclínica) en la que sólo una de las cadenas de átomos de vanadio forma dímeros y la fase T (triclínica) intermedia entre M1 y M2. Las dos fases monoclínicas tienen propiedades aislantes similares. La mayor diferencia en la celda unidad entre las tres fases R, M1 y M2 es la distancia interatómica en el eje longitudinal de las cadenas (eje c de la estructura tipo rutilo), en concreto c(R) = 5,700 Å, c(M1) = 5,755 Å y c(M2) = 5,797 Å.

Para estudiar el punto triple del dióxido de vanadio se comprime una nanobarra en la dirección del eje de las cadenas de átomos de vanadio mientras se cambia la temperatura. El punto triple ocurre a una temperatura de 65,0 ± 0,1 °C y se observa gracias a una discontinuidad en el diagrama plano que relaciona la longitud de la nanobarra y la temperatura.

En mi opinión, lo más interesante de este trabajo es que nos recuerda que aún muchas propiedades electrónicas de los materiales sencillos que no sabemos calcular de forma teórica. Se espera que el intento de reproducir mediante simulaciones por ordenador el diagrama de punto triple obtenido en los experimentos permitirá desarrollar una teoría microscópica que explique las transiciones M1-M2 y R-M2, lo que a su vez ayudará a diseñar mejores películas de “materiales inteligentes” para aplicaciones prácticas.

Contar todas las partículas (fundamentales) conocidas es un ejercicio fácil. Las partículas son excitaciones localizadas de campos cuánticos, por lo que parece mejor contar las componentes de dichos campos. También es fácil, aunque hay algunas sutilezas que hay que tener en cuenta. En Twitter, Amarashiki (@riemannium,TSOR) y Alejandro Rivero (@arivero,web) realizaron este ejercicio hace unos días; por cierto, incluyeron al gravitón, una hipotética partícula aún no descubierta (que la mayoría de los físicos creemos que tiene que existir). Seguir los cálculos en Twitter es engorroso, por ello los resumiré en esta entrada. Además, incluiré algunos comentarios adicionales que ellos no han realizado de forma explícita, pero que me parecen interesantes.

Las partículas conocidas son de dos tipos, fermiones (espín 1/2) y bosones (espín 0, 1 y 2); incluyo el gravitón (espín 2), pero no el gravitino (espín 3/2), siendo ambas partículas hipotéticas aún no descubiertas, porque hay evidencia indirecta de la existencia de las ondas gravitatorias, pero no la hay de la supersimetría. Empezaremos contando los fermiones.

Como muestra la figura de arriba, los fermiones se dividen en tres generaciones de leptones y quarks; en cada generación hay dos leptones, uno cargado (tipo electrón) y otro neutro (tipo neutrino), y hay dos quarks, uno tipo arriba y el otro tipo abajo. Los tres leptones cargados (electrón, muón y tauón) tienen asociado cada uno un neutrino; los seis quarks son llamados arriba, u (up), abajo, d (down), extraño, s (strange), encanto, c (charm), fondo, b (bottom), y cima, t (top). La figura de arriba muestra 12 bolitas que corresponden a 12 partículas (aunque faltan sus correspondientes 12 antipartículas). Sin embargo, hay que recordar que los quarks tienen carga de color (con tres valores posibles), luego en lugar de 6 quarks tenemos 18 (y sus correspondientes 18 antiquarks). Por tanto, un cálculo naïve (ingenuo) nos dice que hay 24 fermiones y 24 antifermiones, un total de 48 partículas.

El cálculo anterior del número de fermiones no tiene en cuenta la quiralidad del modelo estándar. Sabemos que hay electrones levógiros (izquierdos, L) y dextrógiros (derechos, R), pero sólo hemos observado neutrinos levógiros. De hecho, las componentes levógiras se agrupan en parejas (dobletes), pero las dextrógiras no se emparejan (singletes). Por todo ello es mucho mejor contar el número de componentes de los campos que el número de partículas.

Un fermión de Dirac tiene cuatro componentes agrupadas en dos parejas, una pareja representa la partícula y la otra su antipartícula; en cada pareja hay una componente levógira y otra dextrógira. Los tres leptones cargados y los 18 quarks son campos fermiónicos de Dirac y cada uno tiene cuatro componentes. Sin embargo, no sabemos si los leptones neutros (neutrinos) son fermiones de Dirac (los neutrinos dextrógiros no han sido observados en los experimentos) o de Majorana (un fermión de Majorana tiene sólo dos componentes y es idéntico a su antipartícula); si todo va bien con los nuevos experimentos en curso, en un par de años deberíamos saberlo. Por tanto, si los neutrinos son fermiones de Dirac tenemos 4 × 18 + 4 × 3 + 4 × 3 = 96 componentes de campos fermiónicos (de las que 6 aún no han sido observadas en los experimentos), y si son fermiones de Majorana tenemos 4 × 18 + 4 × 3 + 2 × 3 = 90 componentes (siendo los neutrinos y los antineutrinos la misma partícula).

Ahora le toca el turno a los bosones. A baja energía, tras la rotura espontánea de la simetría electrodébil, tenemos un bosón escalar (espín cero), el bosón de Higgs, doce bosones vectoriales (espín uno), el fotón, los bosones Z, W⁻ y W⁺, y 8 gluones, y creemos que existe un bosón tensorial (espín dos), el gravitón, aún no observado de forma directa. En total tenemos 13 bosones; no hay que contar las antipartículas porque todos los bosones que son neutros son idénticos a su antipartícula, y la antipartícula del W⁻ es el W⁺, y viceversa.

Contemos ahora el número de componentes de los bosones. El campo de un bosón escalar neutro (como el Higgs) tiene una sola componente (y por ello es idéntico a su antipartícula); los bosones escalares cargados (como los Higgs predichos por la supersimetría) tienen dos componentes (el de carga positiva es la antipartícula del de carga negativa y viceversa). Por tanto, el Higgs del modelo estándar cuenta como una sola componente.

El campo de un bosón vectorial sin masa (como el fotón y el gluón) tiene dos componentes (transversales al momento) y el de un bosón vectorial con masa (como los bosones W y Z) tiene tres componentes (dos transversales y una longitudinal). Por tanto, en el modelo estándar tenemos 2 + 8 × 2 + 3 × 3 = 27 componentes de campos vectoriales.

El gravitón es un bosón de espín dos sin masa y por tanto tiene dos componentes (que son transversales al momento). Un gravitón con masa tiene cinco componentes (llamadas polarizaciones) ya que es un bosón de espín dos. Esto último puede resultar sorprendente a algunos lectores, pero se sabe desde el artículo de Fierz y Pauli (1939); el tensor métrico en cuatro dimensiones es simétrico, luego tiene 10 componentes, pero no son linealmente independientes entre sí, ya que se cumplen las identidades de Bianchi, que eliminan cuatro componentes, y la física cuántica requiere que su traza sea nula, lo que elimina una componente más.

Por cierto, Boulware y Deser (1972) afirmaron que las ecuaciones de un gravitón masivo deben incluir un término no lineal que invalida la condición de traza nula, con lo que el gravitón masivo debería tener seis componentes (o polarizaciones); pero según el único candidato firme a teoría cuántica de la gravedad, la teoría de cuerdas, el gravitón tiene cinco componentes. Finalmente, como nos recordó Amarashiki en Twitter, en D dimensiones el tensor métrico (una matriz real simétrica) tiene D(D+1)/2 componentes independientes, el campo de un gravitón sin masa tiene D(D−3)/2 componentes y el de un gravitón masivo D(D−1)/2 − 1; por ejemplo, en D=11 dimensiones el campo de un gravitón sin masa tiene 44 componentes.

Resumiendo el número de componentes de los campos bosónicos conocidos es de 1+27+2 = 30. Siendo el número total de componentes (fermiónicas y bosónicas) es de 126. Este número puede ocultar alguna simetría (como proponen Alejandro Rivero y muchos otros físicos), o bien puede ser una simple casualidad. Me permito argumentar a favor de esta última idea.

En cuanto al número de fermiones, no tenemos ningún argumento físico razonable que explique por qué hay sólo tres generaciones de partículas. Por ello, en los experimentos del LHC se siguen buscando partículas de una posible cuarta generación (como también se buscaron en Tevatrón y en LEP). Sin embargo, hay poca esperanza de encontrarlas. Sabemos que el neutrino de la cuarta generación debe tener una masa mayor de 45 GeV, luego será un neutrino muy diferente a los otros tres. Los tests de precisión electrodébil apuntan a la diferencia de masa entre la pareja de quarks de cuarta generación sea pequeña, menor que la masa del bosón W, m(t’) − m(b’) < m(W), con lo que sus desintegraciones más probables son t’→Wb y b’→tW, en las que han sido buscados sin éxito reultando m(t’)>650 GeV y m(b’)>660 GeV ambos al 95% CL (Andrew Ivanov (ATLAS, CMS), “Limits on Fourth Generation Fermions,” arXiv:1308.3084, Subm. 14 Agu 2013). Finalmente, el estudio de los canales de desintegración del Higgs también descarta una cuarta generación de quarks con masas menores de de unos 650 GeV.

Tampoco sabemos si existen o no nuevos bosones vectoriales neutros, Z’ (Z-prima), o cargados, W’ (W-prima), que corresponderían a nuevas simetrías U(1) y SU(2), respectivamente, a incorporar al modelo estándar. Las búsquedas de estos bosones en el LHC los descartan con masas inferiores a 1 TeV (en algunos canales de búsqueda de hasta 2 TeV). Tampoco sabemos si existen nuevos bosones escalares (nuevos bosones de Higgs). Y no he mencionado la posibilidad de partículas más exóticas.

Sólo hemos explorado el modelo estándar por debajo de un 1 TeV (y todavía no de forma completa). En mi opinión, como la de muchos físicos, pensar que lo que hemos descubierto hasta ahora es lo único que existe es muy discutible. Otra cosa muy diferente es que dichos descubrimientos estén a la vuelta de la esquina. Acabamos de iniciar el siglo XXI y todavía no hemos completado el modelo estándar (aún no conocemos muchas de las propiedades de los neutrinos y hay muchas predicciones del modelo estándar que aún no han sido verificadas). Hay que darle tiempo al tiempo. Pero con toda seguridad habrá sorpresas, aunque no sé si llegaré a verlas en la primera mitad del siglo XXI.

Se llaman ventanas “inteligentes” a las que tienen un vidrio que absorbe de forma selectiva la luz visible y el infrarrojo cercano cuando se le aplica un voltaje, cambiando su grado de transparencia a la luz y al calor exterior. Estas ventanas inteligentes permiten reducir la demanda energética de un edificio (en iluminación y climatización). Jaume Gazquez (ICMAB-CSIC, Univ. Aut. Barcelona) y varios colegas de la Univ. California en Berkeley publican en Nature un nuevo material electrocrómico compuesto de nanocristales de óxido de indio y estaño (ITO) incrustados en un vidrio de óxido de niobio. Una de las ventajas más interesantes del nuevo material es que permite un control separado de la absorción de luz en el visible y en el infrarrojo cercano, es decir, en una ventana inteligente se podrán controlar de forma separada e independiente la transparencia óptica y térmica. El rendimiento del nuevo material es mucho mejor de lo esperado, aunque hay resolver algunas cuestiones técnicas antes de que este nuevo material pueda ser usado en ventanas en nuestras viviendas (hay que seleccionar mejores materiales para los electrodos y conviene usar un electrolito sólido en lugar de líquido). Aún así, se trata de un trabajo muy prometedor. Nos lo cuenta Brian A. Korgel, “Materials science: Composite for smarter windows,” Nature 500: 278–279, 15 Aug 2013, que se hace eco del artículo técnico de Anna Llordés, Guillermo Garcia, Jaume Gazquez, Delia J. Milliron, “Tunable near-infrared and visible-light transmittance in nanocrystal-in-glass composites,” Nature 500: 323–326, 15 Aug 2013.

Anna Llordés et al. han desarrollado una nueva técnica de síntesis para incrustar las nanopartículas en el vidrio. Los nanocristales de óxido de indio y estaño (ITO) se recubren de polioxometalatos (POM), cúmulos de cationes metálicos y aniones oxo unidos por enlaces covalentes a la superficie del ITO. Estos nanocristales se condensan y forman una película, que recibe un tratamiento térmico (se calienta a unos 400 ºC), para luego empaquetarlos de forma densa en un óxido de niobio (NbO) dentro de la matriz de vidrio. Sin entrar en detalles técnicos, el método de fabricación de Llordés y sus colegas proporciona un control riguroso de la distribución de tamaño y espacial de los nanocristales en el vidrio. Esto último es muy importante porque el orden estructural de los nanocristales mejora mucho las propiedades electrocrómicas de la matriz de vidrio.

Un estudio financiado por la Comisión Europea afirma que el 50% de los artículos científicos publicados en 2011 y más del 43% de todos los publicados desde 2004 están, a día de hoy, disponibles en acceso abierto (gratuito) en la web. ¿Está cambiando el panorama de la publicación científica? Unos verán el vaso medio lleno y otros medio vacío. En mi opinión este resultado no es debido al movimiento open access per se, si no a la dinámica natural de la web, que ya forma parte íntegra del trabajo de muchos científicos. El informe es Eric Archambault et al. (Science-Metrix), “Proportion of Open Access Peer-Reviewed Papers at the European and World Levels—2004-2011,” European Commission DG Research & Innovation, August 2013 [PDF]. Recomiendo leer a Richard Van Noorden, “Half of 2011 papers now free to read. Boost for advocates of open-access research articles,” Nature 500: 386–387, 22 Aug 2013, y Jocelyn Kaiser, “Half of All Papers Now Free in Some Form, Study Claims,” Science 341: 830, 23 Aug 2013. En español recomiendo “El acceso abierto a las publicaciones de investigación alcanza el llamado «punto sin retorno»,” Comunicado de Prensa de la Comisión Europea, 21 Ago 2013. 

En el estudio, realizado por la empresa canadiense Science-Metrix, se tomó una muestra aleatoria de 20.000 artículos publicados en 2008 en la base de datos Scopus (casi todos publicados en revistas de la editorial Elsevier). Se utilizó un robot de búsqueda (diseñado por Yassine Gargouri, Univ. Quebec en Montreal, Canadá) para encontrar de forma automática dichos artículos en la web. El 32% de los artículos estaban en acceso abierto en diciembre de 2012. Luego se seleccionaron 500 artículos para ser verificados a mano (por una persona utilizando Google) y la cifra se elevó al 48%. Tras esta prueba piloto, el software automático de Science-Metrix se aplicó a 320.000 artículos publicados entre 2004 y 2011, encontrando un promedio del 43% de artículos disponibles en la web de forma gratuita (el porcentaje varía según el país y según la materia científica). El famoso 50% proviene de un ajuste estadístico realizado al 43% observado basado en los resultados de la prueba inicial (los detalles están en el informe). 

¿Cuál es la razón detrás de este porcentaje? El auge de las revistas de acceso abierto sólo explica una pequeña parte (el porcentaje de artículos en estas revistas respecto al total creció del 4% en 2004 al 12% en 2011). La razón última es un cambio de hábito en los propios científicos. 

Cada día hay más grupos de investigación y científicos con página web donde publican sus manuscritos (preprints). Todo científico sabe que su prestigio depende de su número de citas que reciban sus artículos y que éstas dependen de lo fácil o difícil que sea acceder a sus artículos; para los publicados en las revistas de mayor prestigio no hay problema, pero los publicados en las demás revistas acaban siendo ignorados porque nadie puede acceder a ellos. Por ello muchos científicos están publicando sus manuscritos en la web y muchas revistas, buscando incrementar su índice de impacto, también están colocando en acceso abierto muchos de sus artículos (tras un cierto periodo de embargo con acceso limitado sólo a suscriptores).

Además, también ayudan las iniciativas de la Casa Blanca en EEUU (desde febrero de 2013) y de la Comisión Europea (a partir de 2014) que recomiendan que todos los resultados de las investigaciones financiadas por fondos públicos sean de libre acceso (al menos tras un plazo de 12 meses tras la publicación en revista). Con estas iniciativas el miedo de muchos investigadores a represalias por parte de las editoriales de revistas por publicar sus manuscritos en sus páginas web quedan disipadas.

Por supuesto, los expertos en bibliometría tienen serias dudas sobre los resultados del estudio de la empresa Science-Metrix. La metodología utilizada en el informe es muy discutible y muchos expertos creen que el porcentaje real debe rondar el 30% en lugar del 50%. Sin embargo, el porcentaje es lo de menos, un simple número redondo (aunque la noticia y su titular es dicho porcentaje).

Lo importante es que hay una tendencia clara hacia el libro acceso a toda la producción científica, favorecida por los gobiernos, contra la que las grandes editoriales no podrán luchar. La respuesta más natural es el embargo de la información durante entre 6 y 12 meses para proteger los ingresos de suscripción (ya muchas revistas lo están haciendo, como Science y Nature). ¿Qué pasará dentro de 10 años? No lo sé, pero auguro que casi el 100% de los nuevos artículos estarán en acceso abierto un año después de su publicación.

En una torre de cinco o seis dados se inserta una moneda cuyo diámetro sea mayor que sus lados (sirve una moneda de 1 euro o de 50 céntimos). El problema consiste en quitar la moneda utilizando sólo un bolígrafo dejando la torre intacta. Parece imposible, a primera vista, pero, muchas veces, la física permite hacer lo que parece imposible. ¿Cómo crees que se puede hacer? Nos lo cuentan Michael Vollmer y Klaus-Peter Möllmann (Univ. de Ciencias Aplicadas de Brandenburgo, Alemania), “Removing Coins from a Dice Tower: No Magic — Just Physics,” The Physics Teacher 51: 212, Apr 2013 [pdf gratis].

El experimento es fácil de realizar si se conoce el “truco” por lo que puede ser propuesto por los profesores de física a sus alumnos. La clave es usar un bolígrafo recargable que tenga un muelle. Como muestra el vídeo de youtube y esta figura, se utiliza el muelle para proyectar la recarga de tinta; con un poco de práctica se logra controlar el lanzamiento para que sea horizontal y golpee la moneda (sin golpear los dados) por la parte superior. La ley de la inercia hará el resto. La moneda se acelera y los dados reciben sólo un pequeño impulso debido a su fricción con el relieve de la moneda; al salir la moneda se crea un pequeño espacio de aire entre los dados que se cierra entre 12 y 15 milisegundos más tarde. El proceso es muy rápido (el vídeo de youtube se ha grabado a 3000 fps).

Gracias al vídeo de alta velocidad se pueden realizar medidas cuantitativas. El muelle trasladó la recarga de tinta unos 7 mm en unos 6 ms, es decir, la velocidad promedio fue de 1,2 m/s. Con otros bolígrafos estos valores pueden ser diferentes. La recarga de tinta tocó la moneda durante unos 3 ms, acelerándola hasta una velocidad de unos 1,1 m/s cuando todavía está dentro de la torre de monedas. Por tanto, la aceleración fue de alrededor de 370 m/s², es decir, unos 37 g. Debido a la fricción con los dados, la moneda pierde parte de su energía cinética y justo al salir de la torre su velocidad horizontal es de unos 0,9 m/s. Tras salir de la torre, la moneda sigue una trayectoria parabólica. Colocando la torre de dados en el borde una mesa se puede hacer el experimento para que los alumnos puedan medir esta trayectoria (altura, distancia recorrida y duración) con objeto de comprobar las leyes del tiro parabólico.

En resumen, un bonito “truco” basado en la física que puede ser la justificación ideal para un experimento de laboratorio para que los profesores ilustren las leyes de la inercia y del tiro parabólico a sus alumnos.